傳感器的基本特性(知識點)
傳感器的基本特性(知識點)
知識點 1 傳感器的基本特性
傳感器的基本特性是指傳感器的輸入-輸出關系特性,是傳感器的內部結構參數(shù)作用關系的外部特性表現(xiàn)。不同的傳感器有不同的內部結構參數(shù),決定了它們具有不同的外部特性。
傳感器所測量的物理量基本上有兩種形式:穩(wěn)態(tài)(靜態(tài)或準靜態(tài))和動態(tài)(周期變化或瞬態(tài))。前者的信號不隨時間變化(或變化很緩慢);后者的信號是隨時間變化而變化的。傳感器所表現(xiàn)出來的輸入-輸出特性存在靜態(tài)特性和動態(tài)特性。
知識點 2 傳感器的靜態(tài)特性
傳感器的靜態(tài)特性是它在穩(wěn)態(tài)信號作用下的輸入-輸出關系。靜態(tài)特性所描述的傳感器的輸入-輸出關系式中不含時間變量。
衡量傳感器靜態(tài)特性的主要指標是線性度、靈敏度、分辨率、遲滯、重復性和漂移。
線性度
線性度(Linearity)是指傳感器的輸出與輸入間成線性關系的程度。傳感器的實際輸入-輸出特性大都具有一定程度的非線性,在輸入量變化范圍不大的條件下,可以用切線或割線擬合、過零旋轉擬合、端點平移擬合等來近似地代表實際曲線的一段,這就是傳感器非線性特性的“線性化”。所采用的直線稱為擬合直線,實際特性曲線與擬合直線間的偏差稱為傳感器的非線性誤差,取其最大值與輸出滿刻度值(Full Scale,即滿量程)之比作為評價非線性誤差(或線性度)的指標。
靈敏度
靈敏度(Sensitivity)是傳感器在穩(wěn)態(tài)下輸出量變化對輸入量變化的比值。
對于線性傳感器,它的靈敏度就是它的靜態(tài)特性曲線的斜率;非線性傳感器的靈敏度為一變量。
分辨率
分辨率(Resolution)是指傳感器能夠感知或檢測到的最小輸入信號增量,反映傳感器能夠分辨被測量微小變化的能力。分辨率可以用增量的絕對值或增量與滿量程的百分比來表示。
遲滯
遲滯(Hysteresis),也叫回程誤差,是指在相同測量條件下,對應于同一大小的輸入信號,傳感器正(輸入量由小增大)、反(輸入量由大減小)行程的輸出信號大小不相等的現(xiàn)象。產(chǎn)生遲滯的原因:傳感器機械部分存在不可避免的摩擦、間隙、松動、積塵等,引起能
量吸收和消耗。
遲滯特性表明傳感器正、反行程期間輸出-輸入特性曲線不重合的程度。遲滯的大小一般由實驗方法來確定。用正反行程間的最大輸出差值?Hmax 對滿量程輸出YF.S. 的百分比來表示。
重復性
重復性(Repeatability)表示傳感器在輸入量按同一方向作全量程多次測試時所得輸入
-輸出特性曲線一致的程度。實際特性曲線不重復的原因與遲滯的產(chǎn)生原因相同。重復性指標一般采用輸出最大不重復誤差?Rmax 與滿量程輸出YF.S. 的百分比表示。
漂移
漂移(Drift or Shift)是指傳感器在輸入量不變的情況下,輸出量隨時間變化的現(xiàn)象;漂移將影響傳感器的穩(wěn)定性或可靠性(Stability or Reliability)。產(chǎn)生漂移的原因主要有兩個:一是傳感器自身結構參數(shù)發(fā)生老化,如零點漂移(簡稱零漂)。二是在測試過程中周圍環(huán)境(如溫度、濕度、壓力等)發(fā)生變化。這種情況最常見的是溫度漂移(簡稱溫漂)。
知識點 3 傳感器的動態(tài)特性
傳感器的動態(tài)特性是指傳感器對動態(tài)激勵(輸入)的響應(輸出)特性,即其輸出對隨時間變化的輸入量的響應特性。一個動態(tài)特性好的傳感器,其輸出隨時間變化的規(guī)律(輸出變化曲線),將能再現(xiàn)輸入隨時間變化的規(guī)律(輸入變化曲線),即輸出輸入具有相同的時間函數(shù)。但實際上由于制作傳感器的敏感材料對不同的變化會表現(xiàn)出一定程度的慣性(如溫度測量中的熱慣性),因此輸出信號與輸入信號并不具有完全相同的時間函數(shù),這種輸入與輸出間的差異稱為動態(tài)誤差,動態(tài)誤差反映的是慣性延遲所引起的附加誤差。
傳感器的動態(tài)特性可以從時域和頻域兩個方面分別采用瞬態(tài)響應法和頻率響應法來分析。在時域內研究傳感器的響應特性時,一般采用階躍函數(shù);在頻域內研究動態(tài)特性一般是采用正弦函數(shù)。對應的傳感器動態(tài)特性指標分為兩類,即與階躍響應有關的指標和與頻率響應特性有關的指標:(1)在采用階躍輸入研究傳感器的時域動態(tài)特性時,常用延遲時間、上升時間、響應時間、超調量等來表征傳感器的動態(tài)特性。(2)在采用正弦輸入信號研究傳感器的頻域動態(tài)特性時,常用幅頻特性和相頻特性來描述傳感器的動態(tài)特性。
傳感器的數(shù)學模型



?
通常可以用線性時不變系統(tǒng)理論來描述傳感器的動態(tài)特性。從數(shù)學上可以用常系數(shù)線性微分方程(線性定常系統(tǒng))表示傳感器輸出量 y(t) 與輸入量 x(t) 的關系:
d n y

a
n dt n
an?1
d n?1 y dt n?1
?? ? a dy ? a y ? b

1 dt 0 m
d m x dt m
d m?1 x bm?1 dt m?1
?? ? b dx ? b x

1 dt 0
式中: an ,?, a0 和bm ,?, b0 -與系統(tǒng)結構參數(shù)有關的常數(shù)。
(2.6)
線性時不變系統(tǒng)有兩個重要的性質:疊加性和頻率保持特性。
傳遞函數(shù)
對式(2.6)作拉氏變換,并認為輸入 x(t) 和輸出 y(t) 及它們的各階時間導數(shù)的初始值
( t ? 0 時)為 0,則得:
L[ y(t)] Y (s) b sm ? b sm?1 ??? bs ? b
H (s) ? ? ? m m?1 1 0


(2.11)
n n?1 1 0
L[x(t)] X (s) a sn ? a sn?1 ?? ? as ? a
其中: s ? ? ? jw 。
式(2.11)的右邊是一個與輸入 x(t) 無關的表達式,它只與系統(tǒng)結構參數(shù)( a, b )有關,
正如前文所言,傳感器的輸入-輸出關系特性是傳感器內部結構參數(shù)作用關系的外部特性表現(xiàn)。
頻率響應函數(shù)
對于穩(wěn)定的常系數(shù)線性系統(tǒng),可用傅里葉變換代替拉氏變換,相應地有:
H ( jw) ? A(w)e j? ( w)
(2.13)

?H
R
(w) ? H (w)
? ?
2
I
?
2
模(稱為傳感器的幅頻特性):

A(w) ?
H ( jw) ?
(2.14)

相角(稱為傳感器的相頻特性):

?(w) ? arctan HI (w)
HR (w)
(2.15)
傳感器的動態(tài)特性分析
一般可以將大多數(shù)傳感器簡化為一階或二階系統(tǒng)。
一階傳感器的頻率響應
一階傳感器的微分方程為:
dy(t)

a1 dt ? a0 y(t) ? b0 x(t )
它可改寫為:
(2.16)

dy(t)
式中:
? ? dt ? y(t) ? Sn ? x(t)
(2.17)
? -傳感器的時間常數(shù)(具有時間量綱)

A(w) ? 1/ 1 ? (w? )2
這類傳感器的幅頻特性、相頻特性分別為:幅頻特性:
(2.20)
相頻特性:
?(w) ? ?arctan(w? )
(2.21)
圖 2.5 為一階傳感器的頻率響應特性曲線。從式(2.20)、(2.21)和圖 2.5 看出,時間常數(shù)? 越小,此時 A(w) 越接近于常數(shù) 1,?(w) 越接近于 0,因此,頻率響應特性越好。當
w? ?? 1 時:A(w) ≈1,輸出與輸入的幅值幾乎相等,它表明傳感器輸出與輸入為線性關系。
?(w) 很小, tan ?? ? ? ? , ?(w) ? ?w? ,相位差與頻率 w 成線性關系。

2
1.0
0.7
A(?)
0.5
0.4
0.3
0.2
0.1
0.1 0.2
0.5
1.0 2
??
5 10
幅頻特性

0o
?(w)
-20o
-40o
-60o
-80o
0.1
0.2
0.5
1.0 2
??
5 10
相頻特性
圖 2.5 一階傳感器的頻率特性
二階傳感器的頻率響應
典型的二階傳感器的微分方程為:
d 2 y(t)

a
2 dt 2
dy(t)

dt
? a0 y(t) ? a0 x(t )
(2.22)
因此有: 幅頻特性:



?
wn ??
?
wn
?
1
?? 2
w
2 2
? ( )
?
?2
2
w
?
???
?
???
A(w) ? 1? ( ) ? 4
(2.25)
相頻特性:



2? ( w )
wn
1? ( w )2
wn
?(w) ? ?arctan
(2.26)
式中:

a0 a2
wn ? (傳感器的固有角頻率)

a1
2 a0a2
? ? (傳感器的阻尼系數(shù))。
?=0.1
0.2
0.4
1.0 0.6
0.8
10
5
1.0
A(?)
0.5
0.1
0.05
0.01

-40o
-80o
?=0.1
0.2
0.4
0.6
0.8
1.0
-120o
-160o
?(w)
0o
0.10.20.51.02510
? ??n
(a)幅頻特性
0.1 0.2 0.5
1.0 2
? ??n
5 10
(b)相頻特性
圖 2.6二階傳感器的頻率特性
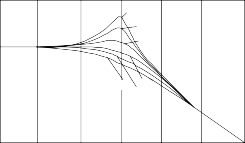
圖 2.6 為二階傳感器的頻率響應特性曲線。從式(2.25)、式(2.26)和圖 2.6 可見,傳感器的頻率響應特性好壞主要取決于傳感器的固有角頻率 wn 和阻尼系數(shù)? 。當 0< ? <
1, wn?? w 時: A(w) ? 1(常數(shù)),?(w) 很小,?(w) ? ?2?
w ,即相位差與頻率 w 成

wn
線性關系,此時,系統(tǒng)的輸出 y(t) 真實準確地再現(xiàn)輸入 x(t) 的波形。
在 w = wn 附近,系統(tǒng)發(fā)生共振,幅頻特性受阻尼系數(shù)影響極大,實際測量時應避免此情況。
通過上面的分析,可得出結論:為了使測試結果能精確地再現(xiàn)被測信號的波形,在傳感
器設計時,必須使其阻尼系數(shù)? <1,固有角頻率 wn 至少應大于被測信號頻率 w 的(3~5)倍,即 wn ? (3 ~ 5)w 。在實際測試中,被測量為非周期信號時,選用和設計傳感器時,保證傳感器固有角頻率 wn 不低于被測信號基頻 w 的 10 倍即可。
a1
一階或二階傳感器的動態(tài)特性參數(shù)
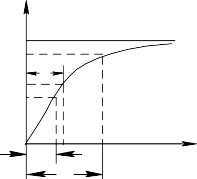
一階或二階傳感器單位階躍響應的時域動態(tài)特性分別如圖 2.7、圖 2.8 所示( Sn =1,A0
=1)。其時域動態(tài)特性參數(shù)描述如下。
y(t)
1.0
0.9
?
0.632
0.5
0
td
tr
t
y(t)
T
1.0 ?
0.9
0.5
td
0
t
r t
t
p
ts
圖 2.7一階傳感器的時域動態(tài)特性
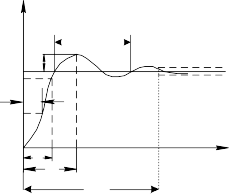
圖 2.8 二階傳感器(? <1)的時域動態(tài)特性時間常數(shù)? :一階傳感器輸出上升到穩(wěn)態(tài)值的 63.2%所需的時間。延遲時間td :傳感器輸出達到穩(wěn)態(tài)值的 50%所需的時間。
上升時間tr :傳感器的輸出達到穩(wěn)態(tài)值的 90%所需的時間。
峰值時間tp :二階傳感器輸出響應曲線達到第一個峰值所需的時間。
響應時間ts :二階傳感器從輸入量開始起作用到輸出指示值進入穩(wěn)態(tài)值所規(guī)定的范圍內所需要的時間。
超調量? :二階傳感器輸出第一次達到穩(wěn)定值后又超出穩(wěn)定值而出現(xiàn)的最大偏差,即二階傳感器輸出超過穩(wěn)定值的最大值。
知識點 4 傳感器的標定與校準
傳感器的標定是利用某種標準儀器對新研制或生產(chǎn)的傳感器進行技術檢定和標度;它是通過實驗建立傳感器輸入量與輸出量間的關系,并確定出不同使用條件下的誤差關系或測量精度。傳感器的校準是指對使用或儲存一段時間后的傳感器性能進行再次測試和校正,校準的方法和要求與標定相同。
傳感器的標定分為靜態(tài)標定和動態(tài)標定兩種。靜態(tài)標定的目的是確定傳感器靜態(tài)特性指標,包括線性度、靈敏度、分辨率、遲滯、重復性等。動態(tài)標定的目的是確定傳感器的動態(tài)特性參數(shù),如頻率響應、時間常數(shù)、固有頻率和阻尼比等。對傳感器的標定是根據(jù)標準儀器與被標定傳感器的測試數(shù)據(jù)進行的,即利用標準儀器產(chǎn)生已知的非電量并輸入到待標定的傳感器中,然后將傳感器的輸出量與輸入的標準量進行比較,從而得到一系列標準數(shù)據(jù)或曲線。
在國內,標定的過程一般分為三級精度:國家計量院進行的標定是一級精度的標準傳遞。在此處標定出的傳感器叫標準傳感器,具有二級精度。用標準傳感器對出廠的傳感器和其他需要校準的傳感器進行標定,得到的傳感器具有三級精度,這就是我們在實際測試中使用的傳感器。
